Trigonometry Questions

Practice True Discount – How many polynomial functions f of degree >=1 satisfy f(X2) = (f(X)) 2 =f(f(X)).147

Practice Trigonometry Questions – A car manufacturer produces only red and blue models which come out of the final testing area completely at random. What are the odds that 5 consecutive cars of the same colour will come through the test area at a time?

Practice Trigonometry Questions – Fishing is a serious environmental issue.It has been determined by the scientists that if the net of a trawler has mesh size x cm by x (square mesh) then the percentage of fish entering the net that are caught in the net is (100-0.02x^2-0.05x.for example if the mesh size is zero 100% of the fish that enter the net will be caught. The trawler with net with a square mesh that was suspected of using an illegal size net dropped its net to the ocean floor near the damans and coast guard officials arrested the crew.the scientists later looked at the size of the fish caught and estimated that the net used by the trawler at least 97.93% of the fish entering the net would be caught. What is the maximum value of x for the net by the trawler?

Practice Trigonometry Questions – In a group of 5 families, every family has a certain number of children, such that the number of children forms an arthmetic progression with a common difference of one, starting with two children in the first family. Despite the objection of their parents every child in a family has three times as many pets to look after as the number of offspring in the family. What is the total number of pets in the entire group of five families.

Practice Trigonometry Questions – In the following star, the numbers on each straight line are in arithmetic progression. What is H+K+L?

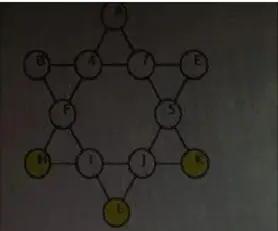
Practice Trigonometry Questions – A property was originally on a 99 years lease and two thirds of the time passed is equal to the four fifth of the time to come.how many years are there to go

Practice Trigonometry Questions – A girl wants to buy a bag. she decides to save her pocket money to buy it. on the first day, she saves Rs.10, and on every subsequent day, she saves Rs.10 more than the money she has saved on the previous day would the girl be able to save Rs.1200 for her bag?

Practice Trigonometry Questions – if a1 = 1/(2*5, a2 = 1/(5*8), a3 = 1/(8*11), …. Then a1 + a2 + a3 + …. + a100

Practice Trigonometry Questions – Let a1, a2, a3n be an arithmetic progression with a1 = 3 and a2 =7. if a1 + a2 + … +a3n = 1830, then what is the smallest positive integer m such that m(a1 + a2 + …. + an) > 1830.

Practice Trigonometry Questions – If the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms, then the ratio of the first term to the common difference is

Practice Trigonometry Questions – if a, b,c and d are integers such that a+b+c+d=30 then the minimum possible value of (a-b)^2 + (a-c)^2 + (a-d)^2 is

Practice Trigonometry Questions – Let a1, a2, a3, a4, a5 be a sequence of five consecutive odd numbers. Consider a new sequence of five consecutive even numbers ending with 2a3. If the sum of the numbers in the new sequence is 450, then a5 is

Practice Trigonometry Questions – An infinite geometric progression a1, a2, a3, … has the property that an = 3(an+1 + an+2 + … ) for every n>= 1. If the sum a1 + a2 + a3 + … + = 32, then a5 is

Practice Trigonometry Questions – A ball dropped from H height and moves 80% of height each time. Total distance covered is

Practice Trigonometry Questions – After striking the floor , a rubber ball rebounds to 4/5th of the height from which it has fallen. Find the total distance that it travels before coming to rest if it has been gently dropped from a height of 120 m.